
A mode can be considered as an inversion of a scale, or a scale within a scale. The major scale consists of seven modes, one based on each scalar degree.
As an example, consider the C major scale (note that in the following examples, I'm not using proper key signatures - keeping a 'plain' stave and annotating the individual notes makes it a bit easier to see what's going on):
Now, we can take a degree of that scale - for example the 2nd degree, D - and examine the major scale based on that note:
Most of the notes of this major scale coincide with notes of the C major scale (the parent major scale) however the 3rd and 7th degrees of the D major scale (F# and C#) do not. This means that the D major scale will not harmonise properly with the C major scale. This problem can be overcome by altering the 3rd and 7th degrees thus:
This new scale, with the formula* 1, 2, b3, 4, 5, 6, b7 has a name: the Dorian mode. As it is built using the 2nd degree of the major scale, it is known as the second mode of the major scale. Therefore, in this example, D Dorian is the 2nd mode of C major.
| * | In an earlier tutorial I mentioned that it was important to understand major scale theory because it is used as a baseline for describing other scales. This is an example of that - we've just described the structure of the Dorian mode with reference to how the scale differs from the parallel major scale. |
It is possible to go though the parent major scale and construct modes off all of the scalar degrees. Each mode has a formula based on how its structure relates to the structure of the parallel major scale (i.e. it shows which of the degrees of that note's major scale have been altered to fit in with the notes of the parent major scale).
When modes are constructed in this way, it is known as the derivative approach. This is to say that all the modes have been derived from one key.
The order in which major scale modes occur is:
| 1st Degree | Ionian Mode |
| 2nd Degree | Dorian Mode |
| 3rd Degree | Phrygian Mode |
| 4th Degree | Lydian Mode |
| 5th Degree | Mixolydian Mode |
| 6th Degree | Aeolian Mode |
| 7th Degree | Locrian Mode |
The table below shows the modes of the C major scale:
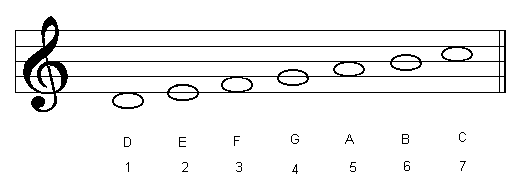
| C Ionian | 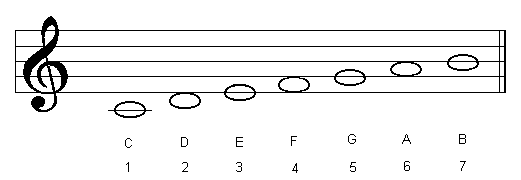 |
| D Dorian |  |
| E Phrygian | 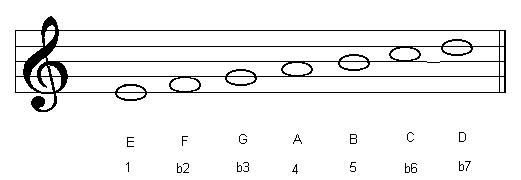 |
| F Lydian | 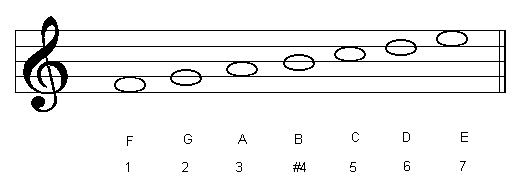 |
| G Mixolydian | 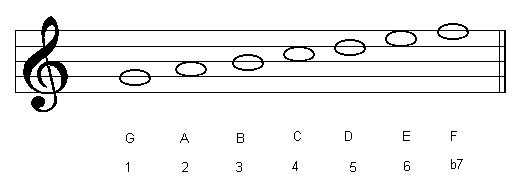 |
| A Aeolian | 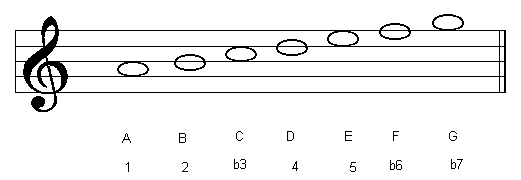 |
| B Locrian | 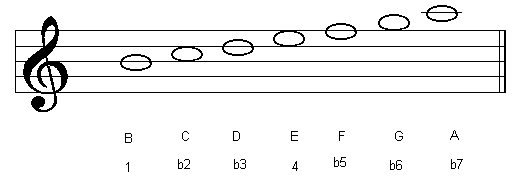 |
The modal sounds can be obtained by playing the notes of a major scale over a certain bass note. If, for example, you play the notes of a C major scale over a C bass note, you hear the Ionian mode; if you play the notes of the C major scale over a D bass note, you hear the D Dorian mode, and so on. This effect arises because the ear is naturally drawn to the lowest note that it can hear.
Each mode has its own distinctive sound. The 1st, 4th and 5th modes (Ionian, Lydian and Mixolydian) have a major sound to them (because of the interval of a major third between the 1 and 3 degrees. The 2nd, 3rd and 6th modes have a minor sound (the flattened third degree gives an interval of a minor third between the 1 and b3 degrees). Although the 7th mode (Locrian) also has a flattened third degree, it cannot be regarded as a minor mode because so many other degrees have been altered (most notably, the flattened 5th degree). This mode is neither major or minor (compare this with the types of triad that exist within the major scale).
We've covered a fair bit of theory here - there's another tutorial which covers some of the practical aspects of all this, namely fingerings for modes on the guitar neck.
That should provide a starting point to modal harmony. More about major scale modes in a later tutorial, plus some modal theory for minor keys, etc., but in the meantime...good luck.
How useful did you find this tutorial?
| Product/Info... | PhatPhish Application | | | Product Help | | | GUPPY - PhatPhish for the web | | | About The Author |
|---|
| Get Stuff... | Download PhatPhish | | | Mechandise | | | Blank Stave And Tab Sheets | | | Tutorials |
|---|
| Do Stuff... | Register | | | Feedback | | | Links | | | Donate | | | Ask A Question |
|---|
| Social Media... | YouTube | | | | |
|---|
| Promote... | Spread The Word | | | Posters/Flyers |
|---|
| Play... | PhatPhish Picks - Boutique Plectrums |
|---|
| ©2002-2022, Dave Dixon / CyberFlotsam http://www.cyberflotsam.com |